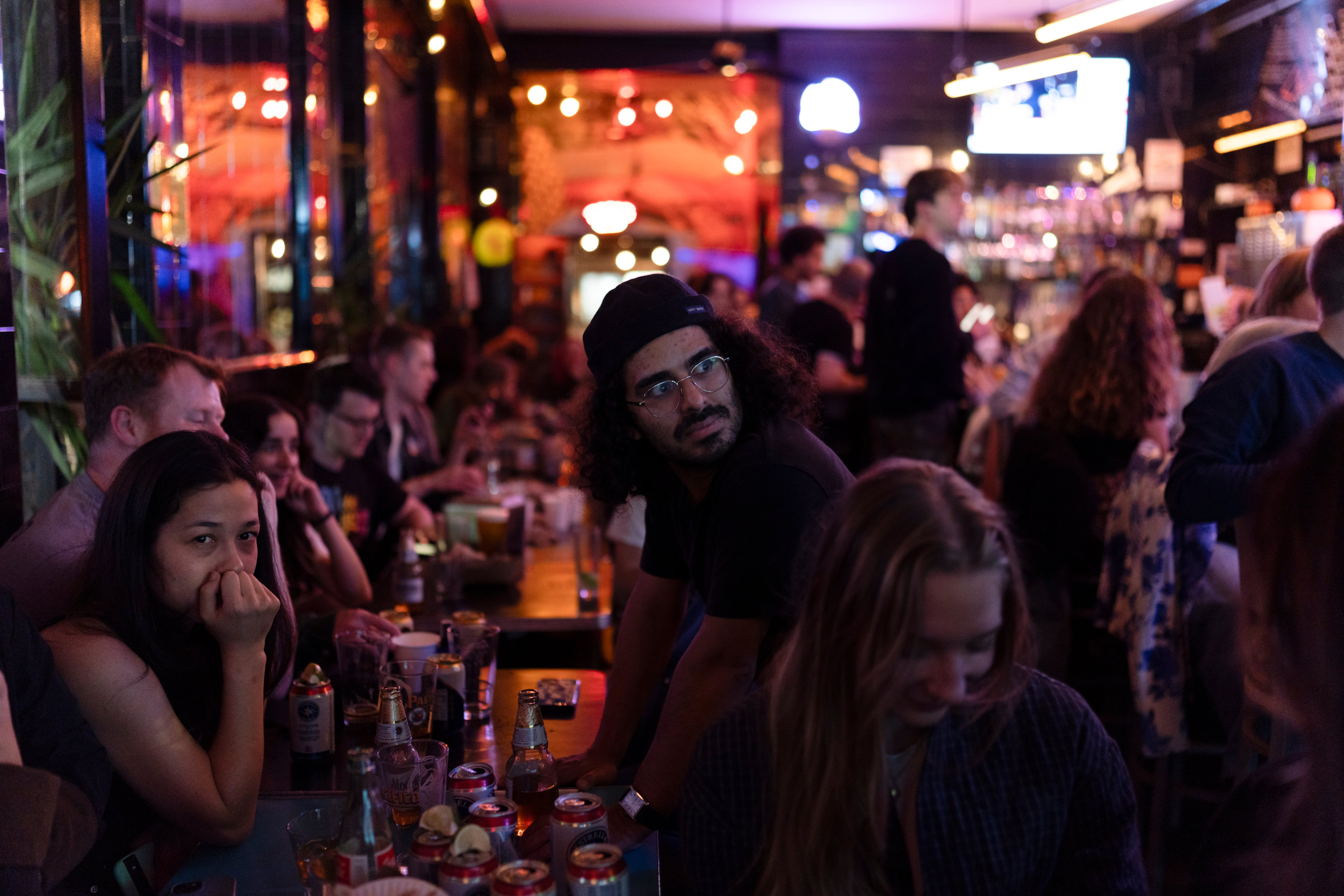
En relación con el “laberinto de alfiles” de la semana pasada, la respuesta es sí: las torres blancas pueden dar jaque mate al solitario rey negro. El primer movimiento de las blancas en el atestado tablero solo puede ser llevar a b2 el alfil de a3 o el de c3, y las negras tienen que mover su rey forzosamente a b7. A partir de ahí se inicia una persecución laberíntica en la que los alfiles blancos han de intentar abrir paso a sus torres y el rey negro solo puede ir por las casillas blancas. ¿Puedes capturarlo?
Si el bar no está muy lleno, es un lugar agradable; si está atestado, no; pero no puedes saber de antemano cuánta gente irá. ¿Cómo tomar una decisión?
En relación con el “laberinto de alfiles” de la semana pasada, la respuesta es sí: las torres blancas pueden dar jaque mate al solitario rey negro. El primer movimiento de las blancas en el atestado tablero solo puede ser llevar a b2 el alfil de a3 o el de c3, y las negras tienen que mover su rey forzosamente a b7. A partir de ahí se inicia una persecución laberíntica en la que los alfiles blancos han de intentar abrir paso a sus torres y el rey negro solo puede ir por las casillas blancas. ¿Puedes capturarlo?
En cuanto al problema de antichess, Salva Fuster encontró una solución en solo 15 jugadas (ver último comentario de la entrega anterior), aunque piensa que tal vez el programa contra el que jugó no hizo en todo momento los movimientos óptimos. ¿Puedes mejorar la estrategia de Stockfish y retrasar la victoria del rey negro?
Fiebre del jueves noche
Y hablando de juegos insólitos y espacios atestados, una lectora mencionó el “problema del bar El Farol”, basado en una anécdota real relativa a un bar de Santa Fe, en Nuevo México, y planteado por el economista William Brian Arthur a finales del siglo pasado. Este es el problema:
El jueves por la noche, todos los habitantes de Santa Fe quieren ir al bar El Farol, siempre que no esté a tope, porque es un local pequeño y es incómodo cuando está atestado. El criterio para ir o no ir es el siguiente:
—Si menos del 60% de la población va a El Farol, es mejor ir al bar que quedarse en casa.
—Si más del 60% de la población va a El Farol, es mejor quedarse en casa que ir al bar.
El problema estriba en que no se puede saber de antemano cuánta gente va a ir a El Farol: todo el mundo ha de tomar la decisión de ir o no ir al mismo tiempo y sin saber qué deciden los demás. Y si todos siguen el mismo criterio para tomar su decisión (siempre que no sea al azar, por ejemplo, lanzando una moneda), el resultado es un fracaso colectivo. Si el criterio general sugiere que El Farol no estará atestado, todos acudirán en tropel y estará lleno. Si, por el contrario, el criterio general sugiere que El Farol estará lleno, todos se quedarán en casa y el bar estará vacío.
¿Qué harías si vivieras en Santa Fe? Y si fueras el alcalde o la alcaldesa de la ciudad, ¿se te ocurre alguna propuesta para solucionar el problema?
Un problema similar se plantea a menudo en la vida real a la hora de intentar evitar un atasco cuando solo hay un camino alternativo: si la mayoría de los conductores eligen ese camino alternativo, será ahí donde se produzca el atasco.
Una variante del “problema del atasco” se plantea cuando un elemento externo orienta las decisiones de los conductores. Si, por ejemplo, la Dirección General de Tráfico recomienda evitar una determinada carretera y los conductores hacen caso mayoritariamente, se congestionará la vía alternativa, por lo que en estos casos hay que tener en cuenta una variable que podríamos denominar “índice de obediencia” de la población. Paradójicamente, una población muy atenta a las recomendaciones institucionales produciría, en algunos casos, un efecto contrario al deseado.
El juego de la minoría
Si el problema de El Farol está basado en una situación real, la condición de no saber qué van a hacer los demás parece poco realista: lo normal sería que los habitantes de Santa Fe se comunicaran entre sí antes de tomar la decisión de ir o no. Y, de hecho, esta es una variante del problema, aunque no simplifica la situación tanto como podría parecer a primera vista, porque, entre otras cosas, las personas consultadas pueden mentir. Lo que nos remite al concepto de “juego de minoría”, propuesto por Yi-Cheng Zhang y Damien Challet en el marco de la teoría de juegos. Pero ese es otro artículo.
Ciencia en EL PAÍS